

Far: Luis Guillermo RESTREPO RIVAS
RESUMO Mi pruvas la ekziston de vektorkampo kreita far ĉiu moviĝanta inercia maso, kampo kiu efektivigas forton sur ĉiu alia proksima moviĝanta maso. Tiu-ĉi kampo havas formalan rilaton kun la gravita kampo similan al tia inter la elektra kaj magneta kampoj, do mi proponas la nomon Gravneta por nomi tiun-ĉi kampon. La ekzisto de la Gravneta Kampo estas implicata far la akcepto de la Speciala Teorio de Relativeco, kaj ĝi estas pruvata uzante tiun teorion. Bazite en variantaj gravnetikaj kampoj, kreitaj far masaj fluoj de varianta rapido, oni produktas ondoj gravitaj-gravnetaj. ASERTO Por ĉiu observanto por kiu ekzistas iu masa fluo, ankaŭ ekzitas vektorkampo V ĉirkauanta tiun masfluon. La vektorkampo V produktas, sur ĉiu maso kiu moviĝas kun rapido U' neparalela kun V, forton F, en direkto orta al la ebeno difinita far U' kaj V. La intenso de la kampo V dependas de la denseco kaj rapido de la masfluo, kaj estas inverse proporcia al la distanco ekde la fluo. PRUVO Konsideru la ekziston de la sceno prezentita en la ĉi-sekvanta desegnaĵo, kiu enhavas jenajn objektojn:
 Se c estas la lum-rapido en vakuo, pro la Speciala Teorio de Relativeco, ni scias ke la rapideco U'' de la objekto W relativa al observanto B, skribita kun bazo en la rapidoj U kaj U' estas:  Pro tio, ke neniu rapido povas superi la lum-rapidon en vakuo, sen perdo de ĝeneraleco ni povas esprimi la rapidojn kiel frakcioj de la lum-rapido, tiel ke eblas uzi angulaj funkcioj, jene:  Laŭ tiuj difinoj de alfa, beta kaj gamma, validas la sekvantaj rilatoj:  kaj aplikante tion a la rilato [1] ni atingas: 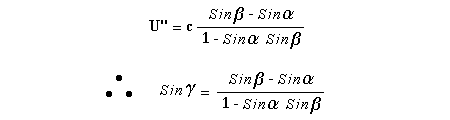 Kaj, pro la fakto ke: Do, anstatŭiginte kaj transforminte, ni sekve atingas:  Nu, ankaŭ veras ke: Do, anstataŭiginte ni alvenas al:  Pensu ni nun pri eta ero de maso apartenanta al la fluo. Tiu ero posedas, laŭ mezuroj de A, longo delta de XA kaj maso delta de M'. Do, la observanto A povas difini la linea denseco de la fluo kiel:  Nu, se delta de M estas la maso en kvieteco (kiel mezurita far B) de la ero de fluo, ni scias ke la maso delta de M' laŭ mezuro far A rilatiĝas kun tiu maso en kvieteco, laŭ Speciala Relativeco, jene:  do, la linea denseco por A ankaŭ estas:  Krome, pro la longo-kurtigo de Lorentz, la longo delta de XA laŭ mezuro de observanto A rilatiĝas kun la koresponda longo en kvieteco delta de XB (laŭ mezuro far B) per la esprimo: Kaj do, esprimita per la kvietecaj maso kaj longo de la flu-ero, laŭ mezuro far B, la linea denseco mezurita far A estas:  Kaj pro tio ke la linea denseco mezurita far B, kvieta relative al la flu-ero, estas:  Do, la rilato inter la lineaj densecoj mezuritaj far A kaj far B estas:  Konsideru ni nun la gravitan kampon kreita far la maso kiun A perceptas kiel "fluo". Se ni supozas ke la longo de tiu maso en la direkto de U estas multege pli granda ol la distanco r, ni vidas ke la intenso de la gravita kampo NB, je la distanco r, mezurita far la observanto B, kvieta relative al tiu maso, estas tia kaŭzita far maso de grandega longo kaj eteta dikeco:  kie G estas la Gravita Konstanto Nu, relative al observamnto B, la objekto W, de kvieteca maso m, posedas maso: ĉar W moviĝas relative al B kun rapido U''. Laŭ tio-ĉi, la forto TB sur m'' kaŭzita far la kvazaŭlineeca distribuo de materio, estas, laŭ mezuro far B: kio egalas al: Kaj simile, en la inercia referenca sistemo de A, la intenso de la gravita kampo NA, je la distanco r, havas amplekson: kiu, anstatŭigante laŭ la rilato [3] devenas: kaj, pro tio ke relative al A, la maso de W estas m', la gravita forto sur W, mezurita far A estas:  kaj ĉar la maso m', rilatiĝas kun la kvieteca maso jene: ni alvenas al:  kio, pro la rilato [4] facile transformiĝas en: kio, pro la rilato [2] egalas al: Kaj pro la trigonometria malegaleco: ni facile konkludas ke que validas la sekvanta malegaleco inter la fortoj sur W mezuritaj far A kaj far B: El la rilato [6] ni atingas: Krome, laŭ la transformado de fortoj de la Speciala Relativeco: Se P estas la plena transversa forto sur iu objekto W, de kvieteca maso m (kia mezuras ĝin observanto kvieta relative al W), do, la plenajn transversajn fortojn PA kaj PB, mezuritaj far observantoj kiuj moviĝas relative al W, kiel A kaj B, oni atingas per la ekvacioj: kiujn ni povas kombini en:  kaj, anstatŭigante la denominatoro laŭ [2] transformiĝas en:  Por la observanto B, la plena forto inter la lineeca maso kaj W etas nur tiu gravita, jene: kaj do: 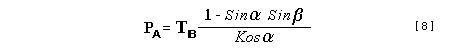 Kaj se ni komparas tiu-ĉi lastan esprimon [8] kun esprimo [6], ni vidas ke en la ĝenerala okazaĵo PA ne egalas al TA Kio kondukas ni al konkludo ke por la observanto A ekzistas alia forto ne perceptebla far B kaj kontraŭa al tiu gravita TA, tiel ke la plena forto mezurita far A estas:kio pro la rilato [8] transformiĝas en:  kaj pro la rilato [7] devenas:  Nun ni povas anstataŭigi la forton TA per la produto de: la kampo NA kaj la maso m', kaj ni atingas: kio, pro la rilato [5] egalas al: Se ni difinas la flua intenso kiel kvanto de maso iranta dum ĉiu tempunuo: Do, la linea denseco mezurita far A, konsiderante diferencialan eron, povas transformiĝi jene:  kaj do: kio se ni reesprimas per la rapidoj, estas: Kaj, se ni difinas la "Gravnetan Konstanton" GN kiel: ni povas esprimi la "Gravnetan Forton" kiel: Ligo: Projekto VIRGO por detektado de gravitogravnetaj ondoj Kopirajto © 1988-2008 Luis Guillermo RESTREPO RIVAS, Ĉiuj Rajtoj Rezervitaj |